Construct a Matrix Whose Column Space Contains

If ABT AT BT show that AB BA. B Find a matrix whose left nullspace contains the vector.

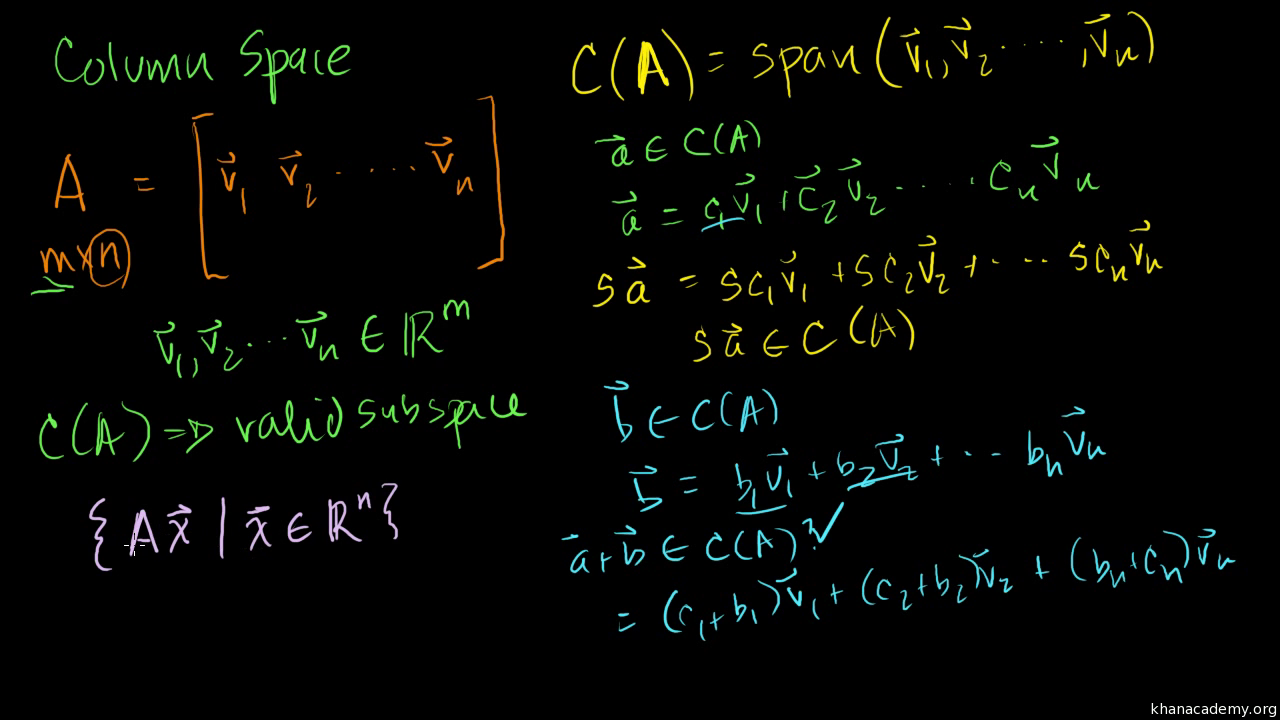
Column Space Of A Matrix Video Khan Academy

Determine the column space of A col A contains all linear combinations of the 3 basis vectors.

. Construct a matrix whose column space contains the vectors 2 0 and whose null space is given by all vectors in the direction of. If ④ Hence. A basis for col A consists of the 3 pivot columns from the original matrix A.

Whose nullspace contains 112. A Show that H is a subspace of R4. A 1 0 a 13 1 3 a 23 5 1 a 33 begin equation Abegin bmatrix 10a_ 13 13a_ 23 51a_ 33 end bmatrix end equation A 1 1 5 0 3 1 a 13 a 23 a 33.

Is a basis for the row space. So you can say you can see from from this Matrix that of the second column is twice off the first column Third column third the third column. Column space of A contain all combination of vectors 1 0 0 0 1 0 0 0 1.

Construct a matrix whose column space contains 111 and whose nullspace is the line of multiples of 1111. 2 pivot columns and 2 free variables only 3 columns. We also know that.

The column space of A is the plane containing all combinations of the pivot columns 1 2 3 and 3 8 7. Ive tried solving it by putting the vectors 1 1 0 0 0 1 as columns in a 3 by 2 matrix and then applying column operations on it to achieve the two vectors 2 5 1 2 to be in two of the. You should answer the two questions.

Taking the first and third columns of the original matrix I find that is a basis for the column space. Row reduce the matrix. Therefore it contains vector 1 1 1.

Apparently the answer is. A Find a matrix whose nullspace contains the vector. Let A 1 0 0 1.

C Find a matrix with column space spanned by and row space spanned by. Space of A and the column space of 2A are the same space. Construct a matrix whose column space contains 1 10 and 011 and whose nullspace contains 101 and 001.

Let u be a fixed nonzero vector in R4 and let H be the set of all vectors x in R4 such that u middot x 0 the dot means dot product. Problems are assigned from the required text. He said um three times on the first call.

That makes Ax b solvable so b is in the column space. Show activity on this post. Way need to apply.

Construct a matrix whose nullspace consists of all combinations of 2210 and 3101. Give an example of A and B. So it stays for any A is m by and the rank of A Because the minority of a its the culture in into this province It gave up its condition.

Construct a 3 by 3 matrix whose column space is only a line. Posted on October 27 2013 by hecker. Construct a matrix whose column space contains 110 and 011 and whose nullspace contains 101 and 001.

Find bases for the row space column space and null space. So it is the ring um to rink nal ity serum. D Given an arbitrary set of three vectors in and a second arbitrary set of three.

The leading coefficients occur in columns 1 and 3. B Find the dimension of H. Construct a matrix whose column space contains vectors 1 1 0 0 0 1 and row space contains vectors 2 5 1 2.

2 A-I I we must hare A. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. Construct a matrix whose column space contains the vectors 2 0 and whose null space is given by all vectors in the direction of.

The problem sets make up 15 of the course grade. Thats the common space. The column space contains all vectors with b 3 b 2-5 b 1 0.

C 3 Thus. Verify this with MATLAB on a 6 by 12 matrix 32 and 33 from section 41. 13 16 17 30 31 and 34 from section 42.

On the other hand AI 1 0 0 1 1 0 0 1 0 0 0 0 so the column space of AI consists only of the zero matrix. 4 points Not possible. Why does no 3 by 3 matrix have a nullspace that equals its column space.

Ill do 36 and negative three. So face make sure excuses three by. If AB 0 then the column space of B is contained in the of A.

Construct a 3 by 3 matrix whose column space contains 1 10 and 101 but not 11 1. Then the column space of A consists of all linear combinations of the vectors 1 0 and 0 1 which is to say all of R2. Since the column space is supposed to contain two independent vectors A must have.

So that there Colin Space its you co two than now space So they arent you go. The columns of a transformation matrix are the images of the basis vectors and the result of left-multiplying a column vector by a matrix is a. We can also produce a matrix that satisfies the conditions of the problem fairly simply and directly without having to invert a matrix by combining the above idea with the following two facts.

This construction is impossible. Problem 2 15 pts Construct a matrix whose column space contains 2 4 1 1 5 3 5 and 2 4 0 3 1 3 5 and whose nullspace contains 2 4 1 1 2 3 5. This is the equation for the plane in the first description of the column space.

Here x 4 is a free variable and x 1 x 2 x 3 are not. Using a b c and d as variables I find that the row reduced matrix says. Determine the column space of A col A contains all linear combinations of the 3 basis vectors.

D The column space of AI equals the column space of A. So if there you go one thing is the dimension of the Colin. Since the nullspace is supposed to contain two independent vectors A can have at most 32 1 pivots.

Construct a matrix whose column space contains 1 1 1 and whose nullspace is the line of multiples of 1 1 1 1. Consider the matrix 1 0 0 1 0 1 0 1 0 0 1 1 Step 2. Construct a matrix whose column space contains 1 1 5 and 0 3 1 and whose null space contains 1 1 2.

13 MATLAB allowed and 17. All columns of A pass this test b 3 b 2-5 b 1 0. Such a matrix A must be 3 3.

Col A c 1 c 2 c 3 c i in R. Easiest way to construct matrix whose colum space contains given vectors is to make those vectors columns of that matrix.

Column Space Calculator

Introduction To Matrices Boundless Algebra

Program To Find The Sum Of Each Row And Each Column Of A Matrix Geeksforgeeks

Column Space Of A Matrix Video Khan Academy